Понятие и расчет эффективной ставки по вкладу. Расчет Эффективной ставки в MS EXCEL
Эффективная процентная ставка по депозиту — это характеристика вклада с капитализацией процентов.
Она отличается от той ставки, которая указана в договоре — номинальной. Ниже мы рассмотрим, как рассчитать эффективную процентную ставку по вкладу, а пока разберемся, что она собой представляет.
По депозиту банк назначает определенную ставку. Она называется номинальной. Если человек оформил вклад без капитализации, то в конце срока он получит начисленные проценты от первоначальной суммы.
Если же клиент выберет , то проценты будут начисляться ежемесячно. При этом они могут выдаваться клиенту или же причисляться к сумме на счете.
В следующем месяце проценты начисляются уже на новую сумму, с начисленными за прошлый месяц. Такая процедура будет повторяться до конца действия вклада.
Конечно же, чем больше сумма на вкладном счете, тем больше процентов будет начислено в итоге. Очевидно, что при одном и том же сроке по вкладам с капитализацией доход существеннее, чем по депозитам с номинальной ставкой.
Эффективная процентная ставка показывает, как приумножаются деньги вкладчика. Она измеряется в процентах и может отличаться от номинальной и в большую, и в меньшую сторону. При помощи эффективной ставки можно сравнить вклады с разными условиями.
Процентная ставка не является показателем прибыльности вклада, нужно также учитывать его свойства. Чтобы узнать доходность по депозиту, следует научиться считать проценты.
Конечно, можно положиться на опыт банковского сотрудника, но важно уметь делать это и самостоятельно, учитывая и процентную ставку, и свойства.
Для расчета применяют две формулы:
- Для расчета простых процентов, которые начисляются в конце срока;
- Для расчета сложных процентов, когда начисление процентов производится ежемесячно (ежеквартально, ежегодно).
Для расчета сложных процентов используют формулу вида: S = (P*I*j / K) / 100.
S — сумма денежных средств, которую получит вкладчик.
P — Первоначальная сумма вложения, а также каждая последующая сумма с учетом процентов, начисленных за прошедший период.
I — процентная ставка годовых.
j — количество дней в периоде, за который производится начисление процентов.
K — количество дней в году.
Пример расчета сложных процентов
Срок вклада — 3 месяца (январь, февраль, март). Процентная ставка — 15% годовых. Первоначальный взнос — 1 000 рублей.
За январь — S = (1 000 * 15 * 31 (день)/ 365) / 100, S = 12.74 рублей.
За февраль — S = (1012,74*15*28 / 365) / 100 = 11.65 рублей (сумма начисленных процентов каждый месяц увеличивается, в данном случае ниже из-за меньшего количества дней в феврале).
За март — S = (1024.39*15*31 / 365) / 100 = 13,05 рублей.
Так с каждым месяцем сумма начисленных процентов все больше, соответственно и доход по депозиту с капитализацией значительно выше.
Часто заемщики сталкиваются с тем, что их расходы по выплате долга существенно превышают на деле суммы, обозначенные улыбчивым кредитным специалистом и зазывающими надписями на рекламных баннерах. Чтобы представлять реальные свои расходы по погашению кредита, прежде всего надо выполнить расчет эффективной процентной ставки. Что это и как ее вычислить, расскажем в этой статье.
Эффективная процентная ставка - это...
Effective rate of interest (эффективная процентная ставка) имеет множество определений, однако все они открывают одну и ту же суть с разных сторон. Это:
- Кредитная ставка, включающая в себя все затраты на обслуживание займа, страховые программы, комиссии и проч.
- Сложнопроцентная годовая ставка, являющаяся величиной оценки доходности определенной финансовой операции.
- Реальная стоимость кредита, которая содержит в себе все затраты заемщика за время погашения долга.
- Действительная стоимость кредита, превышающая номинальную ставку.
Чтобы лучше понять суть эффективной ставки, позже мы проведем небольшую параллель с озвученной номинальной.
Что включает в себя ЭПС по картам
Предупреждаем вас, что самая высокая эффективная процентная ставка ожидает вас при оформлении столь популярной сегодня кредитной карты. ЭПС будет содержать в себе:
- Платеж (комиссию) за выпуск "пластика".
- Комиссию за обслуживание карточки.
- Плату за ведение расчетного счета.
- Комиссию за совершения операций по карте.
- Если уместно - комиссию за конвертацию валюты.
- При нарушениях условий кредитного договора - штраф за превышение лимита или несвоевременное внесение платежа.
- И, собственно, погашение суммы долга и выплату процентов по нему по номинальной ставке.

Отсюда можно сделать следующий вывод: не останавливайтесь на банке, предлагающем самую низкую номинальную ставку. Возможно, в другой организации, где этот показатель несколько выше, эффективная ставка будет на несколько процентов ниже. Из-за чего это может произойти? Из-за отсутствия ряда комиссий (например, за ведение р/с, эмиссию кредитной карточки), "добровольно-принудительной" покупки страховых продуктов на меньшую сумму и т. д. Не стесняйтесь попросить кредитного специалиста озвучить именно ЭПС. И только на основе этой величины подбирать банк-займодателя.
Номинальная и эффективная процентная ставка
Номинальная ставка - это фиксированная величина, размер годовой переплаты за кредит, который вы видите на заманчивых рекламных проспектах. Она не включает в себя стоимость страховок, комиссий, плату за обслуживание кредитной карты - все те растраты, которые вам предстоит понести вместе с выплатой процентов по кредиту и погашением займа.
Почему же клиенту сразу же не озвучивается сумма, которая равна эффективной процентной ставке? Во-первых, эту величину весьма трудно вычислить заранее. Например, если клиент просрочит платеж или несколько взносов, эта величина изменится в большую сторону от той, которая будет рассчитана вначале, из-за начисления пени. А во-вторых, банк попросту растеряет клиентов, если озвучит им все их реальные расходы.

То, что кредитный специалист сообщает клиенту только номинальную ставку, не является обманом или "запудриванием мозгов". Наверняка в вашем кредитном договоре завлекшая вас переплата так и названа - номинальная процентная ставка. Увы, но это упущение именно заемщика, что он перед заключением договора не поинтересовался у операциониста хотя бы примерным размером эффективной годовой процентной ставки.
Номинальная и эффективная ставки относительно вкладов
Что касается банковских вкладов, то здесь в корне другая ситуация:
- Номинальная процентная ставка - фиксированная величина вашего годового дохода, выраженная в процентах. Например, 9 % годовых.
- Эффективная процентная ставка - это плавающая величина вашей прибыли, зависящая от некоторых условий, прописанных в договоре. Что касается вкладов, то она выше номинальной ставки. Это прежде всего характерно для вкладов с капитализацией ("сложными" процентами, начислением процентов на проценты), когда к сумме вклада по прошествии какого-либо периода прибавляется сумма начисленных процентов, и за следующий промежуток времени проценты начисляются на эту уже увеличенную денежную величину. Вклад с 9 % годовых с капитализацией принесет гораздо больше прибыли, чем аналогичный без капитализации. Важно учитывать и ее периодичность: если она происходит каждый месяц, то это гораздо выгодней случая, когда "сложные" проценты начисляются раз в полгода.
А теперь перейдем к "больному" вопросу - кредитам.
Особенности эффективной процентной ставки
ЭПС обязательно должна быть прописана в кредитном договоре - это предписывает Центробанк России. Но многие сталкиваются с тем, что их реальные затраты гораздо выше и этой величины! Происходит это из-за того, что банк рассчитывает ЭПС по формуле, предложенной ЦБ РФ, которая имеет ряд недостатков - в расчет не берутся страховые взносы и некоторые другие ваши убытки.

Предупредим вас, что эффективная процентная ставка - это величина, которая всегда будет выше номинальной даже у идеалистической модели банка, не предлагающего страховые комплекты, комиссии. Причина в том, что тут, так же как и для вкладов, действуют "сложные" проценты и аннуитетные платежи: одна часть уходит на погашение тела долга, а другая - на проценты по нему. То есть за каждый месяц проценты начисляются не только на ту сумму, что вы заняли у банка, но и на величину еще неоплаченных вами процентов.
Вычисление эффективной процентной ставки
Самый верный способ максимально точно представить свои затраты по выплате кредита - это определить эффективную процентную ставку самим, воспользовавшись готовой формулой. Первым делом вам нужно уточнить, с каким промежутком начисляются проценты по вашему займу - каждый месяц, квартал, год, непрерывно и т. д. Ну и, конечно, необходимо знать номинальную ставку по кредиту.
Э = (1 + Н/П) П - 1, где:
- Э - это эффективная процентная ставка:
- Н - номинальная ставка;
- П - количество периодов начисления процентов за один год.
Если же проценты начисляются непрерывно, то подойдет другая формула:
Э = е Н - 1, где:
- Э - эффективная процентная ставка;
- Н - номинальная ставка;
- е - постоянное число, равное 2,718.
Увы, приведенные формулы не предусматривают включения в результат трат, которые вы точно понесете в связи с покупкой страховых продуктов, оформлением справок.

Второй способ вычисления ЭПС
Еще одна формула, по которой можно вычислить эффективную процентную ставку, следующая:
0 = (геометрическая прогрессия) ПВ / (1 + ЭПС) (Д п - Д 1) / 365 ,
где:
- ПВ - размер последней выплаты;
- Д п - дата последнего платежа по кредиту;
- Д 1 - дата первого платежа по кредиту.
Расчеты осложняются тем, что для нахождения ЭПС вам нужно решить это уравнение.

Еще один вариант формулы:
К = П 1 + ((геометрическая прогрессия) П n / (1 + ЭПС) В n , где:
- К - сумма кредита;
- П 1 - первый платеж по займу (необходимо учесть все комиссии, страховые выплаты);
- П n - последний платеж по кредиту (также обязательно нужно включить не только величину погашения тела долга и процентов по нему, но и все побочные платежи);
- ЭПС - эффективная процентная ставка;
- В n - время совершения самого последнего платежа.
- n - месяц выплаты по счету (12-й, 15-й, 36-й и т.д.)
Альтернативные методы подсчета
Формула эффективной процентной ставки - это не единственный путь, который укажет вам ваши реальные траты:
1. Воспользуйтесь онлайн-калькуляторами, в избытке представленными в Сети, - от простых до весьма обстоятельных, учитывающих все платежи.
2. Обратитесь к программе Exel:
- Функция EFFECT() поможет вам произвести расчеты по первой формуле.
- SERIESSUM пригодится для расчетов по второй формуле.

Таким образом можно отметить, что, даже зная номинальную ставку, размер всех комиссий и стоимость страховых продуктов, мы самостоятельно (как, впрочем, и кредитный специалист) сможем высчитать только приблизительную величину ЭПС. Самостоятельные расчеты осложняются "сложными" процентами, платежами-аннуитетами, начислением пени в случае просрочки платежа, чего нельзя предугадать заранее.
Эффективная ставка по вкладу -это характеристика вкладов с системой капитализации процентов. Она отличается от номинальной ставки, указанной в договоре.
Обычный вклад выглядит так. Вкладчик приносит банку деньги во вклад. По вкладу назначают процентную ставку. Эта ставка называется номинальной. Проценты по вкладу начисляют и выплачивают только в конце срока действия вклада.
Вклад с капитализацией процентовимеет иную схему начисления процентов.Проценты по вкладу начисляют ежемесячно. И так же ежемесячно выдают.Но банк неотдаёт деньги вкладчику на руки. А причисляет их к основной сумме вклада. И в следующем месяце проценты начисляются уже на эту новую (возросшую) сумму. Процедура начисление процентов - причисление процентов к сумме вклада будет циклически повторятся ежемесячно до тех пор, пока не закончится срок действия вклада.
Очевидно, что если каждый месяц сумма вклада возрастает, то ежемесячное начисление процентовтоже будет увеличиваться. Так же очевидно, что конечный доход от вклада с капитализацией процентов окажется выше, чем от простого вклада с той же самой номинальной ставкой и с тем же сроком действия.
Настало время проиллюстрировать сказанное на примере.
Некий гражданин положил в банк сто тысяч рублей на год по номинальной ставке в12 процентов годовых. через год он получит прибыль(100000 /100)*12=12000 рублей.
Кто не помнит, как считать проценты от вклада, пожалуйте сюда
Другой гражданин тоже положил в банк на год сто тысяч рублей под 12%, но на вклад с капитализацией процентов.
Расчёт доходов этого гражданина выглядит иначе.12% годовых, это в грубом приближении 1% в месяц
доход за 1-й месяц 10000*0,01=1000
доход за 2-й месяц (100000+1000)*0,01=1010
доход за 3-й месяц (101000+1010)*0,01=1020,1
доход за 4-й месяц (102010+1020,1)*0,01=1030,301
доход за 5-й месяц (103030,3+1030,301) *0,01=1040,61
доход за 6-й месяц (104060+1040,61)*0,01=1051,01
доход за 7-й месяц(105100,61+1051,01)*0,01=1061,51
доход за 8-й месяц (106151,62+1061,51)*0,01=1072,13
доход за 9-й месяц (107231,13+1072,13)*0,01=1083,03
доход за 10-й месяц (108303,26+1083,03)*0,01=1093,86
доход за 11-й месяц (109369,29+1093,86)*0,01=1104,63
доход за 12-й месяц (110463,15+1104,63)*0,01=1115,68
Совокупный доход составил 12682,86 рублей.
Т.е. второй вкладчик по истечении срока вклада получит на 682 рубля больше.
А теперь пересчитаем сколько процентов составляет сумма 12682,86от первоначальных ста тысяч
(12682,86/100000)*100=12,68286%такова итоговая доходность вклада с капитализацией с номинальной ставкой 12% годовых.Эта итоговаядоходность как раз и называется эффективная доходность по вкладу с капитализацией.
Иногда (редко) банки указывают эффективную доходность в договоре. Но по закону они обязаны указывать номинальную ставку. Поэтому эффективную ставку вкладчик вынужден или рассчитывать сам, или довериться банкирам в надежде, что те заплатят честно. Как правило, капитализация увеличивает доходность вклада на 0,5-1,5 процента годовых. Если номинальная доходность в пределах 8-15%, то эффективная ставка, ориентировочно, будет больше на пол-процента, Если номинальная ставка 15% и выше, то капитализация добавляет один процент к доходности. Тридцать процентов годовых и выше - капитализация даёт плюс полтора процента. Всё это грубые прикидки. Надо сказать, что найти на российском рынке депозитов доходность выше 15% уже невозможно. Инфляция снижается, падают и ставки.
Рассчитаем в MS EXCEL эффективную годовую процентную ставку и эффективную ставку по кредиту.
Эффективная ставка возникает, когда имеют место .
Понятие эффективная ставка встречается в нескольких определениях. Например, есть Эффективная (фактическая) годовая
процентная ставка, есть Эффективная ставка по вкладу
(с учетом капитализации), есть Эффективная процентная ставка по потребительским кредитам
. Разберемся, что эти ставки из себя представляют и как их рассчитать в MS EXCEL.
Эффективная (фактическая) годовая процентная ставка
В MS EXCEL есть функция ЭФФЕКТ(номинальная_ставка, кол_пер), которая возвращает эффективную (фактическую) годовую
процентную ставку, если заданы номинальная годовая процентная ставка и количество периодов в году
, в которые начисляются сложные проценты. Под номинальной ставкой здесь понимается, годовая ставка, которая прописывается, например, в договоре на открытие вклада.
Предположим, что начисляются m раз в год. Эффективная годовая процентная ставка дает возможность увидеть, какая годовая ставка позволит достичь такого же финансового результата, что и m-разовое наращение в год по ставке i/m, где i – номинальная ставка.
При сроке контракта 1 год по имеем:
S = Р*(1+i/m)^m – для сложных процентов, где Р – начальная сумма вклада.
S = Р*(1+iэфф) – для простых процентов
Так как финансовый результат S должен быть, по определению, одинаков для обоих случаев, приравниваем оба уравнения и после преобразования получим формулу, приведенную в справке MS EXCEL для функции ЭФФЕКТ()
iэфф =((1+i/m)^m)-1
Примечание . Если задана эффективная годовая процентная ставка, то величина соответствующей ей годовой номинальной процентной ставки рассчитывается по формуле
или с помощью функции НОМИНАЛ(эффективная_ставка, кол_периодов). См. файл примера .
Эффективная ставка по вкладу
Если договор вклада длится, скажем, 3 года, с ежемесячным начислением по сложным процентам по ставке i, то Эффективная ставка по вкладу вычисляется по формуле:
iэфф =((1+i/12)^(12*3)-1)*(1/3)
или через функцию ЭФФЕКТ(): iэфф= ЭФФЕКТ(i*3;3*12)/3
Для вывода формулы справедливы те же рассуждения, что и для годовой ставки:
S = Р*(1+i/m)^(3*m) – для сложных процентов, где Р – начальная сумма вклада.
S = 3*Р*(1+iэфф) – для простых процентов (ежегодной капитализации не происходит, проценты начисляются раз в год (всего 3 раза) всегда на первоначальную сумму вклада).
Если срок вклада =1 году, то Эффективная ставка по вкладу = Эффективной (фактической) годовой процентной ставке (См. файл примера
).
Эффективная процентная ставка по потребительским кредитам
Эффективная ставка по вкладу и Эффективная годовая ставка используются чаще всего для сравнения доходности вкладов в различных банках. Несколько иной смысл закладывается при расчете Эффективной ставки по кредитам, прежде всего по потребительским. Эффективная процентная ставка по кредитам используется для сравнения различные кредитных предложений банков.
Эффективная процентная ставка по кредиту отражает реальную стоимость кредита с точки зрения заёмщика, то есть учитывает все дополнительные выплаты, непосредственно связанные с кредитом (помимо платежей по самому кредиту). Такими дополнительными выплатами являются банковские комиссии - комиссии за открытие и ведение счёта, за приём в кассу наличных денег и т.п., а также страховые выплаты.
По закону банк обязан прописывать в договоре эффективную ставку по кредиту. Но дело в том, что заемщик сразу не видит кредитного договора и поэтому делает свой выбор, ориентируясь лишь на номинальную ставку, указанную в рекламе банка.
Для создания расчетного файла в MS EXCEL воспользуемся Указаниями Центробанка РФ от 13 мая 2008 года № 2008-У «О порядке расчета и доведения до заемщика - физического лица полной стоимости кредита» (приведена Формула и порядок расчета эффективной процентной ставки), а также разъяснительным письмом ЦБ РФ № 175-Т от 26 декабря 2006 года, где можно найти примеры расчета эффективной ставки (см. здесь http://www.cbr.ru/publ/VesnSearch.aspx ).
Эффективную ставку по кредиту рассчитаем используя функцию ЧИСТВНДОХ()
. Для этого нужно составить график платежей по кредиту и включить в него все дополнительные платежи.
Пример
. Рассчитаем Эффективную ставку по кредиту со следующими условиями:
Сумма кредита - 250 тыс. руб., срок - 1 год, дата договора (выдачи кредита) – 17.04.2004, годовая ставка – 15%, число платежей в году по аннуитетной схеме – 12 (ежемесячно). Дополнительные расходы – 1,9% от суммы кредита ежемесячно, разовая комиссия – 3000р. при открытии банковского счета.

Сначала составим График платежей по кредиту с учетом дополнительных расходов (см. файл примера Лист Кредит
).
Затем сформируем Итоговый денежный поток заемщика (суммарные платежи на определенные даты).

Эффективную ставку по кредиту iэфф определим используя функцию ЧИСТВНДОХ (значения, даты, [предп]). В основе этой функции лежит формула:
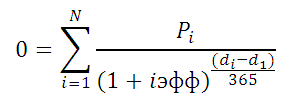
Где, Pi = сумма i-й выплаты заемщиком; di = дата i-й выплаты; d1 = дата 1-й выплаты (начальная дата, на которую дисконтируются все суммы).
Учитывая, что значения итогового денежного потока находятся в диапазоне G22:G34
, а даты выплат в B22:B34
, Эффективная ставка по кредиту для нашего случая может быть вычислена по формуле =ЧИСТВНДОХ(G22:G34;B22:B34)
. Получим 72,24%.
Значения Эффективных ставок используются при сравнении нескольких кредитов: чья ставка меньше, тот кредит и более выгоден заемщику.
Но, что за смысл имеет 72,24%? Может быть это соответствующая ставка по простым процентам? Рассчитаем ее как мы делали в предыдущих разделах:
Мы переплатили 80,77т.р. (в виде процентов и дополнительных платежей) взяв кредит в размере 250т.р. Если рассчитать ставку по методу простых процентов, то она составит 80,77/250*100%=32,3% (срок кредита =1 год). Это значительно больше 15% (ставка по кредиту), и гораздо меньше 72,24%. Значит, это не тот подход, чтобы разобраться в сути эффективной ставке по кредиту.
Теперь вспомним принцип временной стоимости денег: всем понятно, что 100т.р. сегодня – это значительно больше, чем 100т.р. через год при 15% инфляции (или, наоборот - значительно меньше, если имеется альтернатива положить эту сумму в банк под 15%). Для сравнения сумм, относящихся к разным временным периодам используют дисконтирование, т.е. . Вспомнив формулу Эффективной ставки по кредитам, увидим, что для всех платежей по кредитам рассчитывается их приведенная стоимость к моменту выдачи кредита. И, если мы хотим взять в 2-х банках одну и туже сумму, то стоит выбрать тот банк, в котором получается наименьшая приведенная стоимость всех наших платежей в погашение кредита. Почему же тогда не сравнивают более понятные приведенные стоимости, а используют Эффективную ставку? А для того, чтобы сравнивать разные суммы кредита: Эффективная ставка поможет, если в одном банке дают 250т.р. на одних условиях, а в другом 300т.р. на других.
Итак, у нас получилось, что сумма всех наших платежей в погашение основной суммы кредита дисконтированных по ставке 72,24% равна размеру кредита (это из определения эффективной ставки). Если в другом банке для соблюдения этого равенства потребуется дисконтировать суммы платежей идущих на обслуживание долга по бо
льшей ставке, то условия кредитного договора в нем менее выгодны (суммы кредитов могут быть разными). Поэтому, получается, что важнее не само значение Эффективной ставки, а результат сравнения 2-х ставок (конечно, если эффективная ставка значительно превышает ставку по кредиту, то это означает, что имеется значительное количество дополнительных платежей: убрав файле расчета все дополнительные платежи получим эффективную ставку 16,04% вместо 72,24%!).
Примечание . Функция ЧИСТВНДОХ() похожа на ВСД() (используется для расчета ), в которой используется аналогичное дисконтирование регулярных платежей, но на основе номера периода выплаты, а не от количества дней.
Использование эффективной ставки для сравнения кредитных договоров с разными схемами погашения
Представим себе ситуацию, когда в 2-х разных банках нам предлагают взять в кредит одинаковую сумму на одинаковых условиях, но выплата кредита в одном будет осуществляться , а в другом по (равновеликими платежами). Для простоты предположим, что дополнительные платежи не взимаются. Зависит ли значение эффективной ставки от графика погашения? Сразу даем ответ: зависит, но незначительно.
В файле примера на листе Сравнение схем погашения (1год) приведен расчет для 2-х различных графиков погашения (сумма кредита 250 т.р., срок =1 год, выплаты производятся ежемесячно, ставка = 15%).


В случае дифференцированных платежей Эффективная ставка по кредиту = 16,243%, а в случае аннуитета – 16,238%. Разница незначительная, чтобы на ее основании принимать решение. Необходимо определиться какой график погашения больше Вам подходит.
При увеличении срока кредита разница между Эффективными ставками практически не изменяется (см. файл примера Лист Сравнение схем погашения (5лет) ).
Примечание . Эффективная годовая ставка, рассчитанная с помощью функции ЭФФЕКТ() , дает значение 16,075%. При ее расчете не используются размеры фактических платежей, а лишь номинальная ставка и количество периодов капитализации. Если грубо, то получается, что в нашем частном случае (без дополнительных платежей) отличие эффективной ставки по кредиту от номинальной (15%) в основном обусловлено наличием периодов капитализации (самой сутью сложных процентов).
Примечание . Сравнение графиков погашения дифференцированными платежами и по аннуитетной схеме .
Примечание. Эффективную ставку по кредиту можно рассчитать и без функции ЧИСТВНДОХ() - с помощью Подбора параметра. Для этого в файле примера на Листе Кредит создан столбец I (Дисконтированный денежный поток (для Подбора параметра)). В окне инструмента Подбор параметра введите значения указанные на рисунке ниже.

После нажатия кнопки ОК, в ячейке I18 будет рассчитана Эффективная ставка совпадающая, естественно, с результатом формулы ЧИСТВНДОХ() .
Открывая депозит в банке, клиентам стоит обращать внимание не только на размер процентной ставки, но также и на порядок начисления и выплаты процентов, чтобы не только реализовать свою сберегательную стратегию, но и получить максимальный доход. Ведь в действительности эффективная ставка по вкладу может превышать номинальную.
Банки используют два способа выплаты процентов по депозиту - с капитализацией (сложный) и без (простой). По депозитам с простым процентом доход начисляется на другой счет клиента, например карточный или до востребования, и не прибавляется к телу вклада. Проценты могут выплачиваться в конце срока, ежеквартально, ежегодно, ежемесячно или раз в полгода.
Второй вариант - капитализация процентов, или сложный процент, - предусматривает присоединение процентов, которые начисляются, как правило, ежеквартально или ежемесячно к телу вклада. Таким образом, каждое последующее начисление становится больше предыдущего, в результате чего общая доходность по вкладу возрастает.
Любой клиент, используя соответствующие формулы, может самостоятельно посчитать, сколько средств банк должен начислить по вкладам. Впрочем, как на сайтах многих кредитных организаций, так и на сайте Банки.ру и без самостоятельных расчетов выяснить, каким будет доход по вкладам - и с капитализацией, и с простыми процентами.
Очевидно, что при одной и той же номинальной ставке, например 10% годовых, доход по вкладу с капитализацией окажется выше, чем по депозиту с простым процентом. Скажем, доходность годового вклада на сумму 700 000 рублей с ежемесячной капитализацией составит 73 299 рублей, с ежеквартальной - 72 669, с начислением процентов в конце срока - 70 000.
Вот другой пример. Периодичность выплаты процентов по вкладу «Плановый доход» в банке «Глобэкс» - каждые 30 дней. По выбору вкладчика начисленные проценты перечисляются на текущий/карточный счет (простые проценты) либо причисляются к сумме вклада (капитализация - сложные проценты). Базовая ставка по этому вкладу на срок 360 дней и на сумму 100 000 рублей равна 7,75% годовых. За время действия депозита банк начислит 7 643,88 рубля. Эффективная ставка при капитализации процентов составит уже 8,03% годовых, сумма процентов −7 920 рублей.
Еще один пример: депозит «Доступный» в Юниаструм Банке на сумму 50 000 рублей сроком 12 месяцев под 7,5% годовых. Если клиент за весь срок не пополнял и не отзывал часть вклада (что предусмотрено по условиям договора), то в конце срока ему начислят при капитализации процентов 3 880 рублей 61 копейку; при ежемесячном перечислении на текущий счет - 3 749 рублей 11 копеек.
Вице-президент ВТБ 24 Юлия Деменюк считает, что клиентам, не предполагающим снимать проценты в течение срока вклада, стоит выбирать депозиты с капитализацией, так как эффективная процентная ставка по ним будет выше номинальной. Однако ощутимое различие между эффективной ставкой и номинальной будет только при условии, что средства пролежали длительный период времени и проценты по вкладу уплачиваются с определенной периодичностью (например, ежемесячно). Тем же, кто хочет получать на руки ежемесячный или ежеквартальный доход, лучше воспользоваться депозитами, по которым проценты перечисляются на другой счет (без капитализации).
Разница между номинальными и реальными ставками может быть довольно существенной (например, 0,5-1 процентный пункт) и зависит от того, ежемесячно или ежеквартально банк проводит капитализацию процентов. Например, в ВТБ 24 разница между номинальной и эффективной ставкой по рублевым вкладам - в среднем 0,57 процентного пункта, по валютным - до 0,35 пункта; в банке «Глобэкс» по трехлетнему рублевому вкладу разница может составлять 1,2 пункта. Отметим, что в договоре банки указывают только номинальную ставку.
Бывают случаи, когда клиенты не согласны с размером начисленных процентов. По мнению банкиров, в основном это связано с недопониманием того, как рассчитывается налогообложение. Это сейчас ставки достаточно низкие, а полтора-два года назад многие банки предлагали проценты, которые заметно превышали ставку рефинансирования плюс 5%.
«Если вы считаете, что по вкладу вам начислили меньше средств, чем должны были, нужно написать претензию в банк, - говорит начальник отдела депозитных и комиссионных продуктов Промсвязьбанка Мария Плоткина. - Клиенту желательно обосновать свою позицию, в частности привести собственные расчеты. Банк либо предоставит разъяснения, почему он начислил именно такую сумму, либо, если ошибка в расчетах имела место, начислит вкладчику недополученный доход».
Центробанк требует от кредитных организаций ежедневно начислять проценты по вкладам, формально так и происходит - согласно внутрибанковским операциями. Зачисляет же банк проценты де-факто на счет клиента согласно условиям договора.
Выплату процентов банки могут привязать ко дню заключения договора. Например, вклад был открыт 5 февраля, соответственно 5 марта будут начислены проценты (если предусмотрена ежемесячная выплата). «Если день выплаты процентов оказывается выходным, тогда выплата процентов происходит в следующий за ним первый рабочий день, - объясняет начальник отдела банковских продуктов банка «Глобэкс» Ирина Волис. - Например, 30 января - это воскресенье. Значит, проценты будут начислены по 31 января включительно и будут выплачены клиенту 31 января. А в следующем расчетном периоде на один календарный день окажется меньше».
Никаких различий в налогообложении вкладов с простыми процентами и с капитализацией нет. Согласно статье 214.2 Налогового кодекса, доходы частных вкладчиков (резидентов) облагаются налогом в размере 35%, если ставка по рублевому депозиту превышает размер ставки рефинансирования ЦБ плюс 5% (то есть выше 13%), а по валютному, если ставка выше 9% годовых. «Для налогообложения важна только номинальная ставка по вкладу, которая указана в договоре. Даже если эффективная ставка выше 13% (или 9% по валютным депозитам), то налогообложению она не подлежит, - уточняет Деменюк. - Налогообложение производится в момент выплаты процентов по вкладу. Клиент получает проценты за вычетом налога. Банки выступают налоговыми агентами и обязаны взимать налоги с клиента».
Исходя из данных базы вкладов Банки.ру, сейчас в российских кредитных организациях нет ставок выше 12% годовых по рублевым депозитам. Что касается валютных вкладов, то максимальная ставка составляет 9% годовых.
До недавнего времени некоторые банки предлагали 10% годовых по депозитам в валюте. Предположим, что вклад открыт резиденту сроком на 181 день (6 месяцев) на сумму 10 000 долларов.
Вариант 1. Начисление и выплата процентов в конце срока по ставке 10% на сумму 10 000 долларов. Сумма начисленных процентов - 495,89 доллара. Сумма удержанного налога - 17,36 доллара. Сумма к выдаче - 10 478,53 доллара.
Вариант 2. Начисление и выплата процентов проходит ежемесячно по ставке 10%, сумма вклада при открытии - 10 000 долларов. Сумма начисленных процентов - 505,18 доллара. Сумма ежемесячно удержанного налога - 17,67 доллара. Сумма к выдаче - 10 487,51 доллара.
Расчет приблизительный, потому как при исчислении налога на доходы по матвыгоде сумма в валюте умножается на курс ЦБ, установленный на дату проведения операции, и округляется. Отчисление в бюджетную систему осуществляется в рублях.
Положим, ставка по рублевому вкладу равна 15%. Сумма вклада - 100 000 рублей. Срок - 365 дней. Процентный доход - 15 000 рублей. Считаем с учетом 7,75+5 =12,75%: 100 000*12,75%*365/365 = 12 750. Налогообложению по ставке 35% подлежит разница 15 000-12 750=2 250 рублей. Итого налог к уплате - 2250*35% =787,5 рубля.
Вне зависимости от того, как снизилась ставка рефинансирования во время действия вклада, для депозитов сроком до трех лет важно только то, какая ставка ЦБ была на момент заключения или пролонгации договора. Если в этот момент банк предлагал ставку, не подпадающую под налогообложение, то и платить государству ничего не придется.
Наталья РОМАНОВА, сайт
Расчет процентов по вкладу*
Расчет процентов по вкладу по формуле простых процентов
Расчет делается по формуле простых процентов, если проценты начисляются один раз в конце срока вклада:
S = K + (K*P*d/D)/100,
Sp = (K*P*d/D)/100,
где:
Sp - сумма процентов (доход),
K - первоначальная сумма вклада (капитал),
d - количество дней начисления процентов по привлеченному вкладу,
D - количество дней в календарном году (365 или 366).
Расчет процентов по вкладу по формуле сложных процентов
Расчет делается по формуле сложных процентов, если они начисляются на вклад с последующим зачислением на общую сумму депозита (процент на процент):
S = K * (1 + P*d/D/100) N ,
где:
S - сумма вклада с процентами,
К - первоначальная сумма вклада (капитал),
P - годовая процентная ставка,
Сумма процентов (доход) на вклад:
Sp = S - K = K * (1 + P*d/D/100) N - K
Sp = K * ((1 + P*d/D/100) N - 1).
Расчет эффективной процентной ставки по вкладу
Чтобы сравнить доходность вкладов с разной процентной ставкой и на разные сроки при начислении сложного процента, удобно уметь вычислять эффективную процентную ставку в годовом исчислении. Т. е. рассчитать, сколько процентов к начальному вкладу мы получим через год с учетом начисления процентов на процент:
P1 = 100 * ((1+P*d/365/100) N -1),
где:
P - годовая процентная ставка,
d - количество дней в периоде начисления,
N - число периодов начисления процентов.
Пример 1
. Расчет эффективной процентной ставки для вклада на один месяц с годовой ставкой 11%:
100 * ((1+11*30/365/100) 12 -1) = 11,41%.
P = 11,
d = 30,
N = 12.
Пример 2
. Расчет эффективной процентной ставки для вклада на три месяца с годовой ставкой 11%:
100 * ((1+11*90/365/100) 4 -1) = 11,3%.
P = 11,
d = 90,
N = 4.
* Формулы предоставлены Юниаструм Банком.
Дорогие посетители портала Банки.ру! Ждем ваши идеи - о чем бы вам хотелось прочитать в рубрике «Тема дня». Предложения можно оставить в разделе






